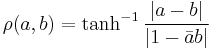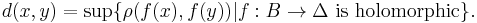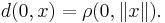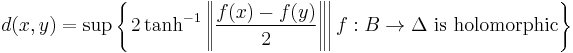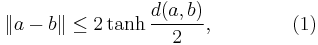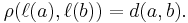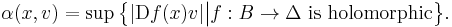Carathéodory metric

In mathematics, the Carathéodory metric is a metric defined on the open unit ball of a complex Banach space that has many similar properties to the Poincaré metric of hyperbolic geometry. It is named after the Greek mathematician Constantin Carathéodory.

1 Definition
2 Properties
3 Carathéodory length of a tangent vector
4 References

Definition

Let (X, || ||) be a complex Banach space and let B be the open unit ball in X. Let Δ denote the open unit disc in the complex plane C, thought of as the Poincaré disc model for 2-dimensional real/1-dimensional complex hyperbolic geometry. Let the Poincaré metric ρ on Δ be given by

$\rho (a, b) = \tanh^{-1} \frac{| a - b |}{|1 - \bar{a} b |}$

(thus fixing the curvature to be −4). Then the Carathéodory metric d on B is defined by

$d (x, y) = \sup \{ \rho (f(x), f(y)) | f�: B \to \Delta \mbox{ is holomorphic} \}.$

What it means for a function on a Banach space to be holomorphic is defined in the article on Infinite dimensional holomorphy.

Properties

For any point x in B,

$d(0, x) = \rho(0, \| x \|).$

d can also be given by the following formula, which Carathéodory attributed to Erhard Schmidt:

$d(x, y) = \sup \left\{ \left. 2 \tanh^{-1} \left\| \frac{f(x) - f(y)}{2} \right\| \right| f�: B \to \Delta \mbox{ is holomorphic} \right\}$

For all a and b in B,

$\| a - b \| \leq 2 \tanh \frac{d(a, b)}{2}, \qquad \qquad (1)$

with equality if and only if either a = b or there exists a bounded linear functional ℓ ∈ X^∗ such that ||ℓ|| = 1, ℓ(a + b) = 0 and

$\rho (\ell (a), \ell (b)) = d(a, b).$

Moreover, any ℓ satisfying these three conditions has |ℓ(a − b)| = ||a − b||.

Also, there is equality in (1) if ||a|| = ||b|| and ||a − b|| = ||a|| + ||b||. One way to do this is to take b = −a.

If there exists a unit vector u in X that is not an extreme point of the closed unit ball in X, then there exist points a and b in B such that there is equality in (1) but b ≠ ±a.

Carathéodory length of a tangent vector

There is an associated notion of Carathéodory length for tangent vectors to the ball B. Let x be a point of B and let v be a tangent vector to B at x; since B is the open unit ball in the vector space X, the tangent space T_xB can be identified with X in a natural way, and v can be thought of as an element of X. Then the Carathéodory length of v at x, denoted α(x, v), is defined by

$\alpha (x, v) = \sup \big\{ | \mathrm{D} f(x) v | \big| f�: B \to \Delta \mbox{ is holomorphic} \big\}.$

One can show that α(x, v) ≥ ||v||, with equality when x = 0.

References

Earle, Clifford J. and Harris, Lawrence A. and Hubbard, John H. and Mitra, Sudeb (2003). "Schwarz's lemma and the Kobayashi and Carathéodory pseudometrics on complex Banach manifolds". In Komori, Y., Markovic, V. and Series, C. (eds). Kleinian groups and hyperbolic 3-manifolds (Warwick, 2001). London Math. Soc. Lecture Note Ser. 299. Cambridge: Cambridge Univ. Press. pp. 363–384.

Carathéodory metric

Contents

Definition

Properties

Carathéodory length of a tangent vector

References